MGD(Mini-batch gradient descent) vs SGD(stochastic gradient descent)
MGD(Mini-batch gradient descent), SGD(stochastic gradient descent)의 차이에 대해 설명하기 위해선 먼저 배치 Batch 가 무엇인지 알아야 한다.
배치 Batch
배치의 사전적 의미는 (일괄적으로 처리되는)집단이다. 배치는 한번에 여러개의 데이터를 묶어서 입력하는 것인데, GPU 의 병렬 연산 기능을 최대한 효율적으로 사용하기 위해 쓰는 방법이다.(GPU 의 병렬연산에 대한 설명 링크)
배치는 Iteration 1회당 사용되는 training data set 의 묶음이며, Iteration 은 정해진 batch size 를 사용하여 학습(forward - backward) 를 반복하는 횟수를 말한다.(철수네 옆집이 영수네 집이고 영수네 옆집이 철수네 옆집 같다.)
예를 들어서, 28x28 픽셀로 구성된 MNIST 데이터로 학습을 하는 경우 1개의 데이터를 사용하는 신경망의 입력과 출력은
(1, 784) → (784, 100) → (100, 50) → (50, 10) → (10, 1)
로 1개의 이미지의 784개 픽셀 데이터를 의미하는 (1,784) 가 입력되고, 1개 이미지 데이터의 10개 숫자에 대한 분류 결과인 (10,1) 이 출력된다.
(엄밀히 따지면 숫자의 표현은 좀 바뀌어야 하지만, 설명의 편의를 위해 위와 같이 작성)
이렇게 한번에 한개의 데이터를 이용하는 방식은 100개의 데이터를 사용해서 학습하기 위해 위와 같은 계산을 100회 반복 해야 하지만 신경망 계산은 기본적으로 행렬 연산이기 때문에, 행렬의 크기만 키워서 입력하면 되는 꼴이므로 아래와 같이
(100, 784) → (784, 100) → (100, 50) → (50, 10) → (10, 100)
계산하여 100개 데이터에 대한 출력을 한번에 얻을 수 있다.
Batch 를 활용하면 GPU 의 병렬연산 기능을 최대한 활용해서 학습 속도를 줄일 수 있는 것이다.
Batch gradient descent(BGD)
전체 데이터 셋에 대한 에러를 구한 뒤 기울기를 한번만 계산하여 모델의 parameter 를 업데이트 하는 방법.
이름에 들어가는 Batch 때문에 혼동스러울 수도 있다.(Ian Goodfellow 또한 자신의 책에서 그렇게 말한다.) 여기서 말하는 batch 는 말 그대로 total training dataset 을 의미한다. 데이터를 분할해서 다룰 때 사용하는 'batch' 라는 단어는 엄밀히 'mini-batch'를 의미하자면 편의상 batch 와 혼용해서 사용하는 것.
처음엔 '한 개의 데이터마다 한 개의 기울기를 구할 수 있는데, 어떻게 전체 데이터 셋에 대해서 기울기를 한번만 구한다는 것인가?' 라는 의문을 가지며 BGD를 잘못 이해하고 있었다.
Gradient descent 라는 알고리즘 자체는 loss function 을 입력 데이터 x 에 대해 편미분해서 기울기를 계산하는 것이 아닌, 가중치 w 에 대해서 편미분을 하는 것이기 때문에, 기울기를 계산하는 것 자체는 입력 데이터 x 의 갯수와 상관이 없다.
에러값을 전체 데이터에 대한 loss function 의 합으로 정의하던 평균으로 정의하던 단순히 w 에 대한 편미분을 수행하면 되는 것.
BGD의 장점
● 전체 데이터에 대해 업데이트가 한번에 이루어지기 때문에 후술할 SGD 보다 업데이트 횟수가 적다. 따라서 전체적인 계산 횟수는 적다.
● 전체 데이터에 대해 error gradient 를 계산하기 때문에 optimal 로의 수렴이 안정적으로 진행된다.
● 병렬 처리에 유리하다.
BGD의 단점
● 한 스텝에 모든 학습 데이터 셋을 사용하므로 학습이 오래 걸린다.
● 전체 학습 데이터에 대한 error 를 모델의 업데이트가 이루어지기 전까지 축적해야 하므로 더 많은 메모리가 필요하다.
● local optimal 상태가 되면 빠져나오기 힘듦(SGD 에서 설명하겠음.)
Stochastic gradient descent(SGD)
추출된 데이터 한 개에 대해서 error gradient 를 계산하고, Gradient descent 알고리즘을 적용하는 방법.
모델의 레이어 층은 하나의 행렬곱으로 생각할 수 있고, 여러개의 묶음 데이터는 행렬이라고 생각 할 수 있다.
즉, 여러개의 묶음 데이터를 특정 레이어 층에 입력하는 것은 행렬 x 행렬로 이해할 수 있는데,
SGD는 입력 데이터 한 개만을 사용하기 때문에 한 개의 데이터를 '벡터' 로 표현하여 특정 레이어 층에 입력하는 것으로 이해할 수 있고 이는 벡터 x 행렬 연산이 된다.
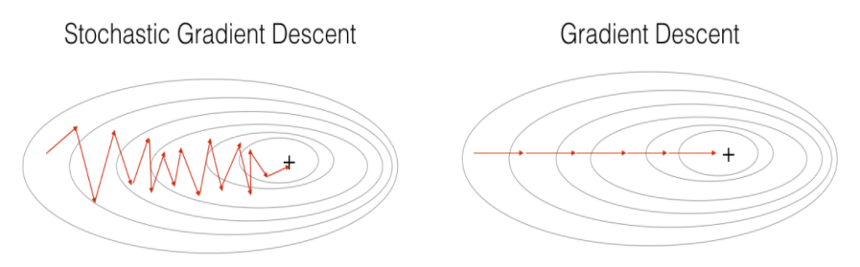
SGD의 장점
● 위 그림에서 보이듯이 Shooting 이 일어나기 때문에 local optimal 에 빠질 리스크가 적다.
● step 에 걸리는 시간이 짧기 때문에 수렴속도가 상대적으로 빠르다.
SGD의 단점
● global optimal 을 찾지 못 할 가능성이 있다.
● 데이터를 한개씩 처리하기 때문에 GPU의 성능을 전부 활용할 수 없다.
Mini-batch gradient descent(MSGD)

엄밀히 따지면 MSGD 와 SGD 는 다른 알고리즘이지만 요즘엔 MSGD를 그냥 SGD라고 많이들 혼용해서 부른다. 그래서 Ian Goodfellow 책에서도 아래 그림처럼 MSGD 알고리즘을 설명할 때 SGD 라고 표현하고 있다.

출처: Deep Learning, Ian Goodfellow, Chap 8. 291pp.
위 알고리즘을 그림으로 간단하게 풀어서 설명하면 아래와 같다.

간단하게 그리다 보니 그림에 도형 갯수는 정확하지 않다. 어쨌든 전체 데이터셋에서 뽑은 Mini-batch 안의 데이터 m 개에 대해서 각 데이터에 대한 기울기를 m 개 구한 뒤, 그것의 평균 기울기를 통해 모델을 업데이트 하는 방법이다.
다시 간단하게 요약하면, BGD 와 SGD 의 장점만 빼먹고 싶은 알고리즘. 전체 데이터 셋을 여러개의 mini-batch 로 나누어, 한 개의 mini-batch 마다 기울기를 구하고 모델을 업데이트 하는 것.
예를들어, 전체 데이터가 1000개인데 batch size 를 10으로 하면 100개의 mini-batch 가 생성되는 것으로, 이 경우 100 iteration 동안 모델이 업데이트 되며 1 epoch 이 끝난다.
MSGD의 장점
● BGD보다 local optimal 에 빠질 리스크가 적다.
● SGD보다 병렬처리에 유리하다.
● 전체 학습데이터가 아닌 일부분의 학습데이터만 사용하기 때문에 메모리 사용이 BGD 보다 적다.
MSGD의 단점
● batch size(mini-batch size) 를 설정해야 한다.
● 에러에 대한 정보를 mini-batch 크기 만큼 축적해서 계산해야 하기 때문에 SGD 보다 메모리 사용이 높다.
batch size 또한 hyper parameter 로써 사용자가 직접 설정해야 하는 값이다. batch size 는 보통 2의 제곱수를 이용하는데, 많은 벡터 계산이 2의 제곱수가 입력될 때 빠르기 때문이다.
source:
'Machine Learning' 카테고리의 다른 글
| Batch Normalization NEED TO CHECK (0) | 2019.09.18 |
|---|---|
| Momentum, AdaGrad, RMSProp, Adam --- NEED TO CHECK (0) | 2019.09.18 |
| Normalization (0) | 2019.09.18 |
| Cross Validation (0) | 2019.09.18 |
| L1 Regularization, L2 Regularization (0) | 2019.09.18 |

댓글